Background Theory

1. Thermal Performance

1.1. U-value

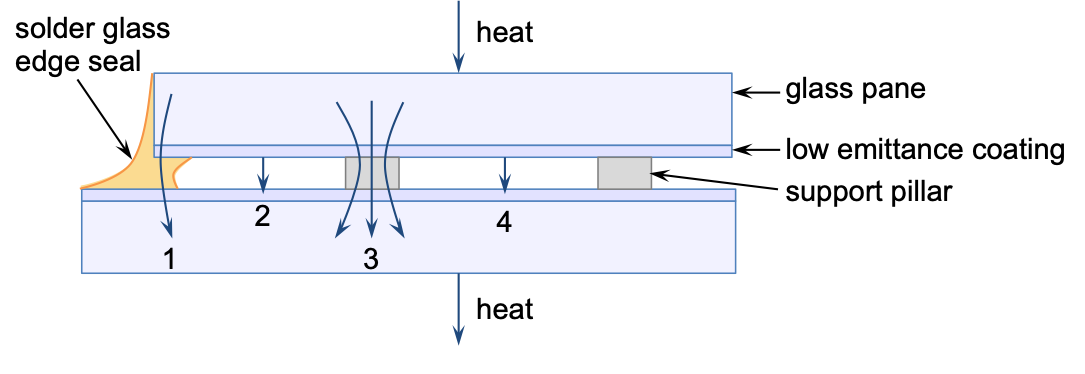
Total heat transfer through the Vacuum Insulated Glazing (VIG), see Figure 1, is a combination of

1. heat conduction through:
• the solder glass edge seal,
• the support pillars and
• the residual gas, and
2. radiation between the glass panes [29].

The overall heat flow ( Q_overall ) for the combined heat pathways can be calculated as: $${Q_{overall}} = {U_{overall}}A{\Delta}T \tag{1.1}\label{eq1.1}$$ where U_overall is the overall heat transfer coefficient (Wm^-2K^-1), A is surface area (m²) and ΔT is temperature difference (K). The overall heat transfer coefficient is also known as the U-value , which is the inverse of the R-value . $$ R-value = RA \tag{1.2}\label{eq1.2}$$ where R is the thermal resistance (W^-1K). If we consider the arbitrary case of multiple thermally connected layers, from 0 to i, the thermal resistance is summed in two parts:

• over the layers using the in series rule $$ R_{total} = R_0 + ... + R_i \tag{1.3}\label{eq1.3}$$
• within each layer using the in parallel rule $${1\over R_{total}} = {1\over R_0} + ... + {1\over R_i} \tag{1.4}\label{eq1.4}$$

In the former, the in series rule applies since removing a layer would break the heat pathway. The in parallel rule applies because removal of an internal pathway would stop heat flow through other existing pathways.

The U-value is widely used as a measure of heat transfer for windows in buildings, although in certain countries, the R-value is the norm. We perform the calculation of U-value according to the ISO 10292 standard. The U-value here is defined as the centre-of-glazing air-to-air thermal conductance of the VIG unit (h_total), which is equal to a sum of inside and outside heat transfer coefficients (h_in and h_out, respectively), the surface-to-surface thermal conductance of the VIG unit (h_VIG) and the thermal conductance of edge seal (h_edge): $$ h_{total} = h_{in} + h_{VIG} + h_{out} + h_{edge} \tag{1.5}\label{eq1.5}$$ According to the ASTM (1991) fenestration test standard, the inside and outside heat transfer coefficients, h_in and h_out, can be defined as 8.3 and 23 W m^-2 K^-1, respectively, for a winter condition. Both coefficients include a radiation contribution of about 4 W m^-2 K^-1. The contribution of conduction/convection is about 4 W m^-2 K^-1 for h_in and about 19 W m^-2 K^-1 for h_out to account for an increase in convection due to forced air flow (wind). $$ {1 \over h_{VIG}} = {1 \over h^{glass}_{inside}} + {1 \over {h_{array} + h_{radiation} + h_{gas}}} + {1 \over h^{glass}_{outside}} \tag{1.6}\label{eq1.6}$$ where h^glass_inside, h^glass_outside, h_array, h_radiation, and h_gas are the thermal conductances of the inside and outside glass sheets, the support pillar array, the surface-to-surface radiation, and the residual gas in the gap, respectively. In all cases the units of thermal conductance are W m^-2 K^-1.

1.2. Thermal conductance of support spacer array (h_array)

The gap between the glass panes in a VIG is maintained through a regular array of support pillars (spacers). Typically, these spacers are cylindrical in geometry with radius r, height h and in an array spacing λ. Each spacer is best represented as a thermal bridge between two λ² areas of glass. The resistance to heat flow through each spacer is a sum of spreading resistance and thermal resistance (conduction) of the spacer: $$ R_{spacer} = {1 \over{2k_{glass}r}} + {h \over{k_{spacer}{\pi}r^2}} \tag{1.7}\label{eg1.7} $$ where k_glass and k_spacer are the thermal conductivities of the glass and spacer, respectively. The spreading resistance is related to the constrained flow that occurs because of the relative size difference between the characteristic length of supported glass, λ, and the radius of the spacer, r. The spreading resistance only depends on the spacer size and the thermal conductivity of the glass. The thermal resistance of the spacer is determined by the length, area and thermal conductivity of the spacer material. Thermal conductance of support pillar array is $$h_{array} = {1 \over{{\lambda}^2R_{spacer}}} \tag{1.8}\label{eq1.8} $$ Increasing the array spacing and spacer height or decreasing the spacer radius can reduce the thermal conductance of the spacer array. Apart from changing the spacer array geometry, the thermal conductance of the array can be lowered by using ceramic or glass materials, instead of metals to form the spacers. However, it is critical to understand that all these parameters affect the mechanical properties of the VIG and should be chosen carefully.

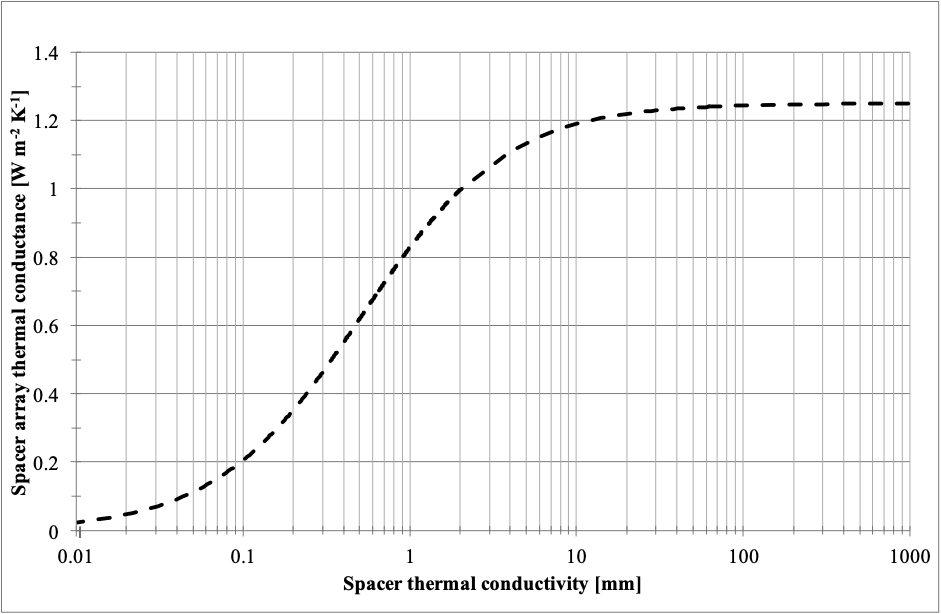
Figure 2 is a plot of the spacer array thermal conductance. It clearly shows how the dominant effect of spreading-to-material conductivity shifts when the thermal conductivity of the spacer material is close to the thermal conductivity of the glass. Increasing the height of the spacer will also increase the thermal resistance. However, there are issues with increasing the overall thickness of the VIG.

1.3. Radiative thermal conductance (h_radiation)

The rate of heat flow between two parallel surfaces due to surface-to-surface radiation (Q_radiation) can be calculated using the Stefan-Boltzman equation for a surface emitting radiation in a vacuum environment $$ Q_{radiation} = {\sigma}{\epsilon}_{eff}A(T_1^4 - T_2^4) \tag{1.9}\label{eq1.9}$$ where σ is the Stefan-Boltzman constant equal to 5.67⋅10^-8 Wm^-2K^-4, ε_eff is the effective emissivity , A is the surface area, and T₁ and T₂ are the temperatures of two surfaces in Kelvin. The effective emissivity of the two surfaces is defined as $${1\over{\epsilon}_{eff}} = {1\over{\epsilon}_1} + {1\over{\epsilon}_2} - 1 \tag{1.10}\label{eq1.10}$$ where ε₁ and ε₂ are the hemispherical emissivities of the two surfaces.

The radiative thermal conductance can be determined by using the average temperature of the surfaces T_average: $$h_{radiation} = 4{\sigma}{\epsilon}_{eff}AT_{average}^3 \tag{1.11}\label{eq1.11}$$ It is important to note that the determination of the emissivity is non-trivial and has spatial and temperature dependence. Nevertheless, numerous studies [1] have shown that equation 1.10 is an accurate description of the emissivity of two plane parallel surfaces, which is the arrangement of the internal surfaces in most, if not all, VIG designs.

1.4. Gaseous conduction (h_gas)

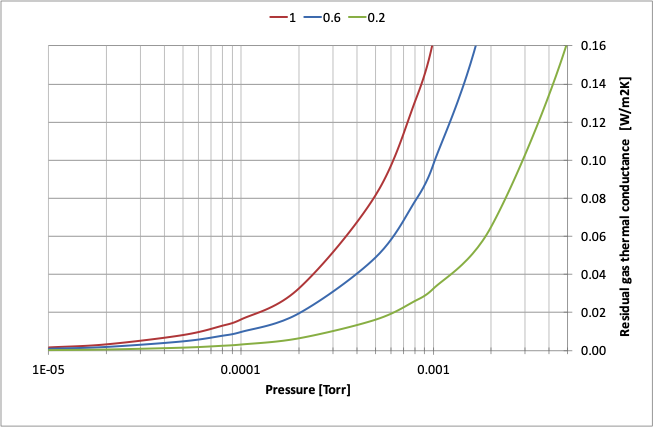
Within the evacuated gap of the VIG, there is always some amount of residual gas, at low pressure, that does result in heat conduction between the inner glass surfaces because of non-equilibrium gaseous energy transport through repeated surface collisions. Since the internal glass surfaces are parallel and separated by a short distance, and relative to the surface area of collisions, the glass panes are of equal area, the gaseous heat conduction can be defined using equation 1.12 per unit area $$ h_{gas} = {\alpha}_cP{{{\gamma}+1}\over{{\gamma}-1}}{\sqrt{R\over{8{\pi}MT_{eff}}}}(T_2 - T_1) \tag{1.12}\label{eq1.12} $$ where γ is the specific heat ratio of the gas, R is the molar gas constant, P is the gas pressure, M is the molecular weight of the gas, T₁ and T₂ are the temperature of surface 1 and 2, T_eff is the ‘effective’ temperature of the gas that is not the average of T₁ and T₂, but is an intermediate value between T₁ and T₂, and α_c is the combined surface condition accommodation coefficient: $$ {\alpha}_c = {{{\alpha}_1{\alpha}_2}\over{{\alpha}_2 + {\alpha}_1(1 - {\alpha}_2)}} \tag{1.13}\label{eq1.13} $$ where α₁ and α₂ are the accommodation coefficients of surface 1 and 2. The accommodation coefficient is representative of the surface related factors that would create a difference in the collision energy exchange as compared to that of an ideal surface interaction; for example, surface roughness, and specifically in the case of the VIG, the use of low emissivity coatings. Even though the parameters in equation 1.12 are dependent on temperature and also on the composition of the gas, the greatest unknown factor in calculating this thermal conductance is the accommodation coefficient. Figure 3 shows the residual gas thermal conductance as a function of pressure for different combined accommodation coefficients. At a pressure of 0.001 Torr, the value of the combined accommodation coefficient does have a strong affect on the thermal conductance. Interestingly, at pressures below 0.0001 Torr, this dependence becomes much weaker. With the potential low contributions, on the order of 0.1 W m^-2 K^-1 of radiation and spacer conduction, it is reasonable to suggest that the VIG vacuum pressure should be at or below 0.0001 Torr. This will reliably produce a negligible gaseous contribution even if the accomodation coefficient is not well defined.

1.5. Thermal conductance of edge seal (h_edge)

In most, if not all, designs of the VIG the edge seal will be a thermal bridge between the glass panes, or at least a point of thermal non-uniformity. Here we assume that the edge seal forms a thermal bridge between the glass panes. This means that the heat flow close to the edges of the unit is greater than the heat flow at the centre of the unit. The actual heat flow is not one dimensional from the hot to the cold side of the edge seal, since at the edge seal, there is a small temperature difference between the panes.

At the edges, the heat flow originates as lateral heat flow along the hot glass sheet (due to the temperature difference between the edge and centre of the glass) and subsequently through the edge seal and along the cold glass sheet. Unlike other thermally insulting window technologies, the contribution to overall heat flow due to the edge seal can be mitigated by covering the edge seal and near glass surfaces with insulating material; that is, using an insulating sash frame with the VIG. The edge contribution has been modeled well numerically and a good analytical model has been derived (both of which have been validated against measurements).

The analytic model (equation 1.14) is a simple method of calculating the magnitude of heat flow due to the edge seal. The model is for a VIG in a window frame (sash) configuration where the sash design provides insulation that extends some distance over the surface of the glass on either side.

The total heat flow per unit length of the edge seal (Q_edge) can be defined as $$ Q_{edge} = {{(T_2 - T_1)k_{glass}t}\over {\sqrt{k_{glass}t\over{h_{in}}} + w_1 + w_2 + \sqrt{k_{glass}t\over{h_{out}}}}} \tag{1.14}\label{eq1.14} $$ where t is glass thicknes, and w₁ and w₂ are edge recess of glass panes 1 and 2, respectively. For a rectangular glazing of dimentions L_x and L_y, the thermal conductance of edge seal can be written as $$ h_{edge} = {{2(L_x + L_y)\over{L_xL_y}}{{k_{glass}t}\over{\sqrt{k_{glass}t\over{h_{in}}} + w_1 + w_2 + \sqrt{k_{glass}t\over{h_{out}}}}}} \tag{1.15}\label{eq1.15} $$

1.6. Agreement between calculated and measured thermal conductance

The fundamental theory of heat transfer described in the previous sections is a reliable definition of the heat flow through a VIG unit. Nevertheless, each of the equations should be considered not ideally, but as applied to a ‘real world’ unit. Typically, the equations applied as defined here will provide results that would be within 15% of measured data for a VIG unit. This difference has been well studied and the following is a brief outline of the discrepancies that exist between these equations and potential direct measurements of thermal heat flow.

1. When summing the heat flow contributions, the contribution of spreading resistance includes the flow through the glass, however, the direct conduction through the spacer does not.
2. The spacer thermal resistance is changed due to surface contact geometry or surface conditioning or a surface coating on the spacer, which impacts the thermal resistance of the spacer.
3. The spacers cover the surface of the glass, and thus, reduce the surface area of radiation. Furthermore, radiation is temperature dependent, and at distance close to a spacer, the surface temperature becomes dependent on the spacer contact. This is radiative suppression due to the spacer thermal bridge, which reduces further the available surface area for radiative transfer.
4. If the spacer height is ill defined and the glass surfaces form close contact, for example, below 80 mm, there may exist a level of evanescent-wave coupling, a surface-to-surface near field interaction.
5. The complete surface-to-surface radiation level should be solved iteratively since it is temperature dependent and depends only on the internal vacuum side surfaces of the glass panes, and would only be well-defined at steady state.
6. When performing a direct thermal conductance measurement on a VIG, the surface non-uniform temperature distribution over the glass surfaces must be taken into consideration for well-defined results.

2. Mechanical Performance

2.1. Temperature Difference Load

A temperature difference across the VIG produces mechanical stresses in the glass sheets due to the expansion of the hot glass sheet relative to the cold glass sheet. Since the standard solder glass edge seal fixes rigidly the glass panes, tensile and compressive stresses cause bending of the VIG. Reasonable estimates of the magnitude of the temperature-induced stresses can be obtained using an analytic model [30].

In applying the analytic solution, we assume that

• the both glass sheets have the same thickness,
• the glass panes are square,
• the temperature of each glass sheet is uniform,
• each sheet bends into a spherical shape,
• the stresses due to bending at the mid-plane of each sheet are zero and
• the edges of the VIG unit are unconstrained.

The last two conditions are appropriate for small amounts of bending, and this bending mode is conventionally referred to as linear bending.

For this simple case, the external surface of the hot glass sheet experiences tensile stresses (σ_t), where the magnitude is estimated using the following equation: $${\sigma}_t = {{E{\alpha}{\Delta}T_a}\over{4(1-{\mu})}} \tag{2.1}\label{eq2.1} $$ where E is the Young’s modulus of the glass, α is the glass coefficient thermal expansion, ΔT_a is the average temperature difference between the glass sheets and μ is Poisson’s ratio of glass. The internal surface of the hot glass sheet experiences compressive stresses of twice the magnitude. Stresses of the same magnitude, but in the opposite sense, exist on the internal and external surfaces of the cold glass sheet, respectively. The bending stress of the VIG can be written as $${{\sigma}_{bend}}={{3\over4}E{\alpha}{\Delta}T_a} \tag{2.2}\label{eq2.2}$$ To estimate the average temperature difference between the glass sheets, we have to define the average temperatures of the cold and hot glass sheets (T_ac and T_ah, respectively). $${{\Delta}T_a}=T_{ah}-T_{ac} \tag{2.3}\label{eq2.3}$$ $${T_{ah}}={T_e+(T_{gh}-T_e)(1-{{4\sqrt{{\lambda}tR_h}}\over{L}})} \tag{2.4}\label{eq2.4} $$ where T_e is temperature of the edge, T_gh is temperature of the hot glass sheet, λ is thermal resistance of glass, t is the thickness of the glass sheet, R_h is the thermal resistance of the hot side (inverse to heat transfer coefficient of the hot side) and L is glass length. $$ {T_{ac}}={T_e - (T_e - T_{gc})(1-{{4\sqrt{{\lambda}tR_c}}\over{L}})} \tag{2.5}\label{eq2.5} $$ where T_gc is temperature of the cold glass sheet and R_c is the thermal resistance of the cold side. $${T_{gh}}={T_c + (T_h - T_c){{R_c + R_{VIG}}\over{R_c + R_{VIG} + R_h}}} \tag{2.6}\label{eq2.6} $$ where T_c and T_h are air temperatures on the cold and hot sides, respectively, and R_VIG is the thermal resistance of the VIG. $${T_{gc}}={T_c + (T_h - T_c){R_c\over{R_c + R_{VIG} + R_h}}} \tag{2.7}\label{eq2.7} $$ $$T_e = {T_{gc}+{{(T_{gh}-T_{gc})\sqrt{R_c}}\over{\sqrt{R_c}+\sqrt{R_h}}}} \tag{2.8}\label{eq2.8} $$ If the heat transfer coefficients on each side of the vacuum insulating glass are different, the mean temperature of the glazing T_m can be different from the temperature of the edge. $${T_m}={(T_{ah}+T_{ac})\over2} \tag{2.9}\label{eq2.9} $$ In such a situation, an additional "hoop" stresses exist in the edge region of the VIG. The hoop stress is uniform through the thickness of the bonded edge seal and is parallel to the edges of the VIG unit. If T_e < T_m , the hoop stress (σ_hoop) is tensile and its magnitude can be estimated using $${{\sigma}_{hoop}}=E{\alpha}(T_e - T_m) \tag{2.10}\label{eq2.10} $$ The total temperature-induced stress of the VIG is a sum of bending and hoop stresses.

2.2. Atmospheric Pressure Load

2.2.1. Introduction

A primary aim of a Vacuum Insulated Glazing (VIG) is to hold a vacuum environment between the glass panes. In doing so the glass panes are subjected to atmospheric pressure over its whole service lifetime. This pressure is uniform over the glass surface, where there is a pressure difference between the internal and external environments. To minimize residual gas contribution to the thermal performance of the VIG, the pressure should be at 0.001 Torr or less. Nevertheless, the forces resulting from atmospheric pressure act in full at pressures at 100 Torr since atmospheric pressure is about 760 Torr. These forces produce the following stresses in the VIG:

1. The spacers used to maintain the gap between the glass panes will experience a compressive load, which will be proportional to the array spacing;
2. Due to the compressive load on the spacers, there will also be an indentation load at the glass surface from the spacer contact;
3. Since there are areas over the glass surface that are no directly supported by spacers, there will be glass bending between the spacers resulting in
• a stress on the outside glass surfaces which are directly above the spacers adjacent and
• a stress over the inside glass surfaces between the spacers.
4. The glass region between the edge seal and the first row of pillars will also deform and will result in a built-in stress at the edge, which will depend on the stiffness and geometry of the edge seal.

Figure 1 is an illustration that maps the region where the high levels of tensile stress are expected, and in the following discussion analytical solutions to estimate these stresses are presented.

Note: it is very difficult to extend the scope of this document, and calculator, to include all potential variations in materials, geometries, and methods of incorporation, of components into a VIG that would affect the stresses of interest. Therefore, it is the focus of the discussions below to limit the outcomes to cylindrical spacers, and to an edge that is rigid and well-defined (i.e. solder glass edge seal).

2.2.2. Spacer Compression

The applied load on a spacer in a VIG is dependent on the atmospheric pressure over the glass surfaces. Each spacer is within an area of glass that is equal to the distance between the spacers (the array dimension). This means that the applied force on a spacer is given by $${F_s}={\sigma}_{atm}{\lambda}^2 \tag{2.11}\label{eq2.11} $$ where F_s is the applied force in N, σ_atm is atmospheric pressure (0.1 MPa) and λ is the array spacing or distance between spacers in mm. For a cylindrical spacer that is r mm in radius, the average compressive stress (σ_comp) in the pillar would then be given as $${\sigma_{comp}}={{{\sigma}_{atm}{\lambda}^2}\over{{\pi}r^2}} \tag{2.12}\label{eq2.12} $$ For the spacers, under atmospheric pressure, the compressive load is uniform and leads to the two main forms of failure depending on the material of the spacer; plastic or brittle failure. As with all other types of structural applications, the use of metals means that failure, at least initially, is a process of yielding which is in the beginning an irreversible deformation of the structure. In terms of brittle failure, at the critical stress limit the structure exhibits catastrophic failure or breakage. This is no different in the use of metals or ceramics as materials for the spacers.

Typically, the spacers are produced from metals; stainless steel alloys or Inconel alloys. These materials will yield when a critical force is reached. It is practically of best practice to take the yielding of the spacers as the failure of the spacer, rather than a splitting, or shearing, breakage of the spacer. As will be discussed below, for metal spacers, the failure of the glass is typically of greater concern. This means that for a stainless steel, for example type 304, the yield stress would be taken as about 200 MPa, but can be as high as 500 MPa and for the Inconel alloy as high as 1000 MPa. Clearly, using equation 2.12 this leads to limits on the diameter of the spacer relative to the array dimension, which will now be apart of the criteria of the acceptable level of heat flow due to the whole spacer array.

2.2.3. Indentation Contact Stress

The indentation process is a well-studied area of interest in many industries. In the VIG we have the simple case, when considering a metal spacer, of a rigid object pushing into a softer flat surface. Ultimately, we are concerned with the initiation and subsequent propagation of cracks in the glass due to the spacer contact. Even though it is important to understand the effect of the contact surface cracks, under the action of atmospheric pressure we are primarily concerned with defining the critical load at which cracks will initiate.

For fracture of the glass surface to occur a favorably located and orientated flaw must be within the tensile surface stress zone near the edge of the spacer contact. It has been shown that the critical load (F_c) for the initiation of surface fracture in the glass is best given by $${F_c}={\sqrt{{{\pi}^3E{\beta}{\gamma}r^3}\over{2(1-{\nu}){\Phi}_r}}} \tag{2.13}\label{eq2.13}$$ where E is the Young’s modulus of glass, ν the Poisson’s ratio of glass, γ the surface energy of glass, β a factor that represents the effect of the static contact friction of spacer-to-glass (it is equal to 1 for no friction, and increases in a non-linear manner for a friction coefficient less than 1), and Φ_r the energy function, which describes the energetics of the fracture process. It is important to note that, typically, the use of clean glass surfaces, that are also now in a dry low pressure vacuum environment, will produce static coefficients of friction near or at 1, for most materials that will come into contact with the glass surface, unless a special low friction material is used. Furthermore, a non-zero friction coefficient will result in a reduction in the magnitude of the contact stress on the glass, if there are no shear forces acting on the spacer.

In using the typical values for soda-lime float glass, and the known energetics of the fracture process, it is simple to determine the critical load for glass fracture. When the equations are rearranged to include the atmospheric force on a unit cell of glass over a spacer, the critical failure load can be approximated with respect to the spacer radius and array spacing as (assuming no friction over the contact) $${\lambda}{\lt}{155r^{3/4}} \tag{2.14}\label{eq2.14}$$ It is interesting to note that this expression does not include information about the glass thickness, and this is expected, since the contact area will always be much smaller than the array spacing for the practical VIG designs.

Furthermore, as will be noted in the next section too, the fact that the contact surface of the glass is in the vacuum environment reduces the probability of fracture. Equation 2.14, in the defined fracture energy of the glass and the energy function of the fracture process, does consider that the environment is a dry low-pressure environment.

2.2.4. Bending of the Unsupported Glass Areas

UNDER CONSTRUCTION

2.2.5. VIG Design Optimization under Atmospheric Pressure Load

The Atmospheric Pressure Load Calculator provides a plot of the VIG U-value as a function of support pillar array spacing. The plot is interactive. The values of the array spacing and U-value are shown when you hover your mouse over the red curve. The plot also shows the curves representing the differences between the compressive surface stress on the glass and the fracture strength limit for compression of the spacer and the contact pressure between the spacer and glass surfaces. You can use them to find an optimal array spacing which will combine the lowest U-value with acceptable stresses (below the fracture strength limit). Simply, the optimum design is found at the point where the U-value curve intersects the curve corresponding to Contact Fracture Limit or Above Spacer Fracture Limit or any other limit (whichever comes first), indicates the maximum allowed array spacing.

UNDER CONSTRUCTION

2.3. Debris Load

The failure of Vacuum Insulated Glazing (VIG) during ‘debris’ (impulse) impact is almost always caused by the extension of shear cracks at the support pillars under bending stresses in the glass sheets. In other cases, the stresses over the glass surface (due to bending) near the center and close to the edge seal result in catastrophic failure. Although debris impact can be defined by many parameters such as size, material and velocity of the debris and angle of incidence, here we will use the well-known “ball drop” test configuration to represent a simple simulation of debris impact. We assume that the energy of the impact is at low velocity and the glass bending stresses and the maximum glass pane deflection originate from a central impact of a stainless steel ball that is dropped from a stationary position above a VIG and falls under the influence of gravity alone, from a specific height. The VIG unit is placed horizontal and is rectangular in shape and simply supported at the edges. It is also assumed that the ball applies only a vertical force to the VIG unit and the radius of the area of contact between the ball and the plate is much smaller than the distance between two neighboring support pillars, so the contact force between the ball and the plate can be modeled as a point load.

As the total VIG thickness is much smaller than the VIG unit dimensions in the x- and y-directions, the VIG can be considered as a composite thin plate. To adjust the thin plate model and account for shear forces affecting the support pillars, we divide the VIG into two areas (see Figure 1):

• far from the point of the impact, the VIG is assumed to behave as a single plate with a thickness of 2h_glass;
• in the locality of the impact, the upper and lower glass plates of the VIG are treated as two independent plates coupled by vertical forces transmitted through the support pillars.

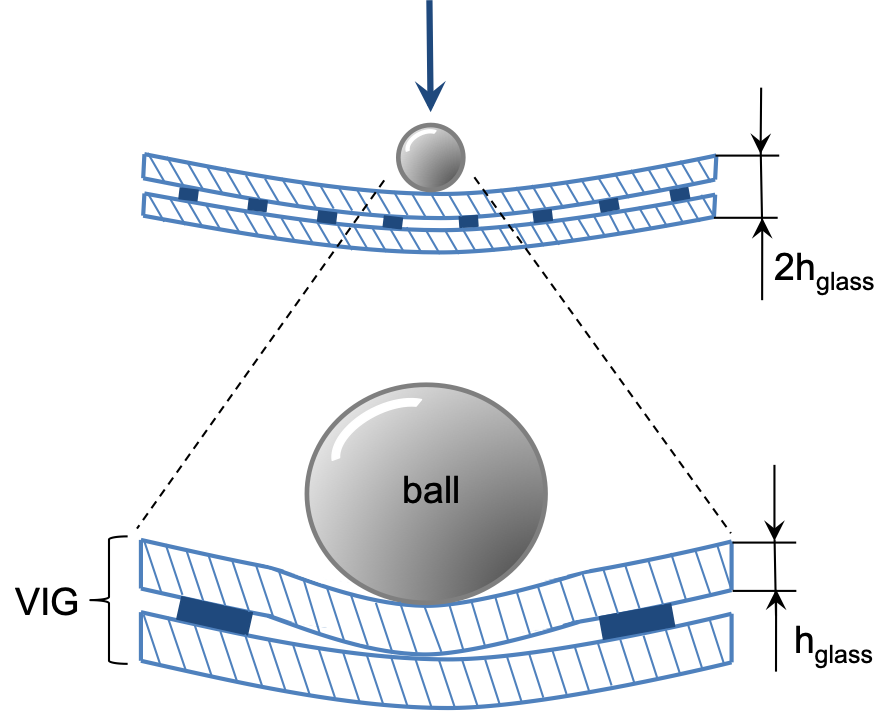
The deflection of the VIG (W_VIG) is assumed to be a sum of the deflection of the single plate with 2h_glass thickness (W_2h) and the deflection due to the specific distribution of loads on the upper plate alone (W^*). $${W_{VIG}}=W_{2h}+W^* \tag{2.15}\label{eq2.15} $$ Let us first consider the response of a single glass plate to an impulse load.

2.3.1. Response of a thin plate to an impulse impact

The deflection of a thin plate can be calculated using the Germain-Lagrange equation: $${ {{{\partial}^4W}\over{{\partial}x^4}}+2{{{\partial}^4W}\over{{\partial}x^2{\partial}y^2}}+{{{\partial}^4W}\over{{\partial}y^4}}}={q(x,y)\over D} \tag{2.16}\label{eq2.16} $$ where w is the thin plate deflection, q(x, y) is the vertical load applied to the point (x, y) and D is the flexural stiffness of the plate. $$D={{Eh_{glass}^3}\over{12(1-{\mu}^2)}} \tag{2.17}\label{eq2.17} $$ where E is Young’s modulus of the plate, h_glass is thickness of the plate and μ is Poisson’s ratio of the plate. The Navier method gives the solution to equation 2.16 as a double trigonometric Fourier series: $${W(x, y)}={\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}A_{ij}sin{{i{\pi}x}\over{L_x}}sin{{j{\pi}y}\over{L_y}}} \tag{2.18}\label{eq2.18} $$ where L_x and L_y are VIG dimensions in the x- and y-directions, respectively, and A_ij are Fourier series coefficients.

The boundary conditions for a simply supported plate: \begin{cases} W=0; {{{{\partial}^2W}\over{{\partial}x^2}}+{\mu}{{{\partial}^2W}\over{{\partial}y^2}}}=0, & \text{at x=0 and $x=L_x$} \\ W=0; {{{{\partial}^2W}\over{{\partial}y^2}}+{\mu}{{{\partial}^2W}\over{{\partial}x^2}}}=0, & \text{at y=0 and $y=L_y$ } \tag{2.19}\label{eq2.19} \end{cases} Let us expand the loading function q(x, y) into a double trigonometric Fourier series: $${q(x,y)}={\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}a_{ij}sin{{i{\pi}x}\over{L_x}}sin{{j{\pi}y}\over{L_y}}} \tag{2.20}\label{eq2.20}$$ In the case of impulse impact at the point with coordinates (x_o, y_o), the coefficients a_ij and A_ij are defined as $${a_{ij}}={{{4F}\over{L_xL_y}}sin{{i{\pi}x_o}\over{L_x}}sin{{j{\pi}y_o}\over{L_y}}} \tag{2.21}\label{eq2.21}$$ $${A_{ij}}={{1\over{{\pi}^4}D}{{a_{ij}}\over{({i^2\over{L_x^2}}+{j^2\over{L_y^2}})^2}}} \tag{2.22}\label{eq2.22}$$ and the deflection can be found as $${W(x,y)}={{{4F}\over{{\pi}^4L_xL_yD}}\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}{{1}\over{ij({i^2\over{L_x^2}}+{j^2\over{L_y^2}})^2}}sin{{i{\pi}x_o}\over{L_x}}sin{{j{\pi}y_o}\over{L_y}}sin{{i{\pi}x}\over{L_x}}sin{{j{\pi}y}\over{L_y}}} \tag{2.23}\label{eq2.23}$$ where F is applied force. $$F(t)=\begin{cases} F_{max}{sin}^2{{{\pi}t}\over{\tau}}, & \text{at 0 ≤ t ≤ τ } \\ 0, & \text{at t > τ} \end{cases} \tag{2.24}\label{eq2.24}$$ where F_max is the force amplitude, t is time and τ is impact duration. The force reaches its maximum value (F_max) when the time is equal to half the impact duration, which in turn is equal to π divided by the angular frequency (ω). At this time the plate deflection also reaches a maximum. $${{\tau}\over{2}}={{\pi}\over{\omega}} \tag{2.25}\label{eq2.25}$$ The angular frequency is given by $${\omega}={{\pi}^2({i^2\over{L_x^2}}+{j^2\over{L_y^2}}){\sqrt{D\over{{\rho}h_{glass}}}}} \tag{2.26}\label{eq2.26}$$ where ρ is the glass density.

In contrast, the local force on the glass is equal to the ball impulse (I) at the first moment of ball contact to the glass plate divided by impact duration. $$I=m_{ball}v_0/{\tau} \tag{2.27}\label{eq2.27}$$ where m_ball and v₀ are ball mass and speed, respectively. The speed of the ball at the moment of its contact to the glass plate can be calculated as $${v_0}={\sqrt{2gh_{drop}}} \tag{2.28}\label{eq2.28}$$ where g is gravitational acceleration and hdrop is the height from which the ball drops onto the glass plate. The maximum deflection of the glass plate (W_max) can be estimated using the next equation $${W_{max}}={{{4m_{ball}v_0}\over{{\pi}^3}L_xL_y{\sqrt{D{\rho}h_{glass}}}}\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}{{1}\over{ij({i^2\over{L_x^2}}+{j^2\over{L_y^2}})}}sin{{i{\pi}x_o}\over{L_x}}sin{{j{\pi}y_o}\over{L_y}}sin{{i{\pi}x}\over{L_x}}sin{{j{\pi}y}\over{L_y}}} \tag{2.29}\label{eq2.29}$$

2.3.2. Response of the entire VIG to an impact impulse

Now let us return to equation 2.15 for the deflection of the entire VIG unit. To calculate W_2h in equation 2.15, we simply use 2h_glass thickness in equation 2.17 and equation 2.29. The component W^* is given as $${W^*}={W_{1h}-W_{2profile}-W_{imp}} \tag{2.30}\label{eq2.30}$$ where W_1h is the maximum deflection of a single plate of thickness h_glass (equation 2.29), W_2profile is the maximum deflection of a single plate of thickness h_glass whose time-dependent profile is the same as W_2h, and W_imp is the component which accounts for the impulse transfer from the upper plate to the lower plate. In order to calculate W_2profile, we determine the circumstance under which a single plate of thickness h_glass will adopt the profile W_2h: $${W_{2profile}}={{{\omega}_1\over{{\omega}_2}}W_{2h}} \tag{2.31}\label{eq2.31}$$ where ω₁ and ω₂ are the angular frequencies (equation 2.26) of the plates of thicknesses h_glass and 2h_glass, respectively.

Both upper and lower plates exert forces on each other via the support pillars. As the pillar diameter is much smaller than the size of a unit cell of a pillar and glass, the impulse delivered to the upper plate (I_p) is modeled as an impulse delivered to a point. If the relationship between indentation force and displacement is linear, the impulse is defined as $${I_p(x_p,y_p)}={0.5kW^*(x_p,y_p)dt} \tag{2.32}\label{eq2.32}$$ where k is the equivalent spring constant. Finally, the maximum deflection of the VIG can be estimated as $${W_{VIG}}={W_{2h}+0.25W_{1h}} \tag{2.33}\label{eq2.33}$$

2.3.3. Vertical and lateral forces

Knowing the maximum deflection of the VIG, we can estimate the amplitude of the vertical force (F_v) $${F_v}={W_{VIG}k_{eff}} \tag{2.34}\label{eq2.34}$$ where k_eff is the effective spring constant which is defined as $${k_{eff}}={{k_{glass}k_{pillar}}\over{k_{glass}+k_{pillar}}} \tag{2.35}\label{eq2.35}$$ where k_glass and k_pillar are the spring constants of glass plates and support pillars, respectively. $${k_{pillar}}={{E_{pillar}{\pi}d^2_{pillar}}\over{n_{pillar}h_{pillar}}} \tag{2.36}\label{eq2.36}$$ where E_pillar is the Young’s modulus of a pillar, d_pillar is the pillar diameter, n_pillar is the number of pillars in the unit and h_pillar is the pillar height. We used 0.5 mm pillar diameter and 0.2 mm pillar height for the calculations. $${k_{glass}}={{E_{glass}{\pi}d^2_{pillar}}\over{2h_{glass}}} \tag{2.37}\label{eq2.37}$$ where E_glass is the Young’s modulus of glass.

If the relative lateral displacement of the two glass plates (d_plate) is known, and the pillar is in non-slip contact with the plates, the sideways force at the pillar (F_l) can be calculated by dividing the lateral displacement by the compliance factor for a pillar with glass at both ends. The compliance factor is equal to 4,75x10^-8 mN^-1 for a 0.5 mm diameter pillar on float glass. As the pillar contacts the glass plates at both ends, the compliance factor is double this value. The relative lateral displacement is the lateral distance between a point on the upper glass plate and the point on the lower glass plate that were directly opposite to each other when the VIG was unstressed. $${d_{plate}}={h_m{{{\partial}W_{WIG}}\over{{\partial}s}}} \tag{2.38}\label{eq2.38}$$ where h_m is the vertical distance between the midplanes of the upper and lower plates and s is the displacement in the plane of the VIG in the direction of the impact site. $${{{\partial}W_{VIG}}\over{{\partial}s}}={{1\over{\sqrt{(x_0-x_p)^2+(y_0-y_p)^2}}}((x_0-x_p){{{\partial}W_{VIG}}\over{{\partial}x}}+(y_0-y_p){{{\partial}W_{VIG}}\over{{\partial}y}})} \tag{2.39}\label{eq2.39}$$

2.4. Wind Load

Wind can generate enough pressure to damage windows and walls or uplift a roof and similar horizontal structures. However, we are interested in the effect of wind on VIG only. Therefore, anywhere further in this section, Wind Load means a horizontal wind pressure that can cause glass panes in the vertical VIG to bend or crack.

2.4.1. Wind Pressure

Dynamic wind pressure (P_wind) acting on a glass pane can be written as $$P_{wind} = {{\rho}_{air}{{v_{wind}}^2\over2}} \tag{2.40}\label{eq2.40} $$ where ρ_air is air density and v_wind is wind speed at the building site. At sea level and 21 ^oC, an average air density is 1.2 kg/m³. The air density is lower at higher altitudes than sea level due to lower atmospheric pressure. However, a temperature is also lower in theses locations that compensates the difference in atmospheric pressure [43].

2.4.2. Wind Speed at the Building Site

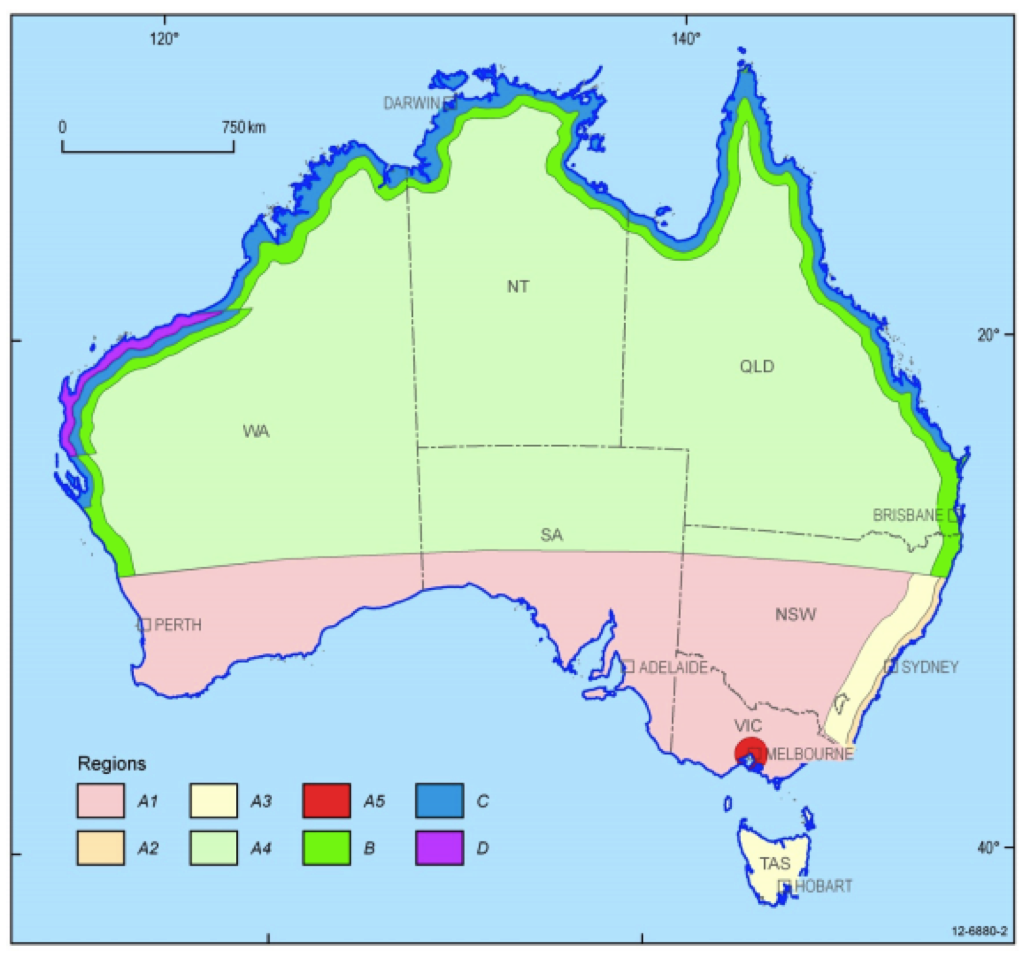
The wind speed at the building site depends on a number of factors including prevalent wind direction, terrain category, height above the ground, shielding and topography [44]. Wind multipliers are used to account for these local conditions. $${v_{wind}}=v_{region}M_dM_{z, cat}M_sM_t \tag{2.41}\label{eq2.41}$$ where v_region is regional wind speed, M_d is wind direction multiplier, M_z,cat is terrain/height multiplier, M_s is shielding multiplier and M_t is topographic multiplier. According to AS/NZS 1170.2, the regional wind speed is a 3-second gust wind speed at the standard meteorological height of 10 meters in open country terrain. The regional wind speed depends on the location with respect to the wind regional map (Figure 5) and recurrence interval (Table 1).

Table 1. Peak gust wind speeds in various wind regions in Australia (AS/NZS 1170.2 standard).

Recurrence	Peak Gust Wind Speed, m/s
interval in years	A	B	C	D
1	30	26	23	23
10	34	33	39	43
50	39	45	55	66
100	41	48	59	73
1000	46	60	74	94

The regional wind speed can be calculated using four following equations: $${v_{region A}}=67 - 41R^{-0.1} \tag{2.42}\label{eq2.42}$$ $${v_{region B}}=106 - 92R^{-0.1} \tag{2.43}\label{eq2.43}$$ $${v_{region C}}=F_C(122 - 104R^{-0.1}) \tag{2.44}\label{eq2.44}$$ $${v_{region D}}=F_D(156 - 142R^{-0.1}) \tag{2.45}\label{eq2.45}$$ where F_C and F_D are additional uncertainty factors equal to 1.05 and 1.1, respectively. The calculated values have to be rounded to the nearest 1 m/s.

2.4.3. Wind direction multiplier (M_d)

In regions B, C and D, the wind direction effect is small as tropical cyclone and thunderstorm gust wind speed dominate the extreme high range tail of the wind speed distribution [4]. For these regions, M_d=1. If the prevalent wind direction is unknown, the wind direction multiplier is also equal to 1. In the other case, the wind direction multiplier should be taken from Table 2.

Table 2. Wind direction multiplier (AS/NZS 1170.2 standard).

Cardinal direction	A1	A2	A3	A4	A5	A6	A7
N	0.90	0.80	0.85	0.90	1.00	0.85	0.90
NE	0.80	0.80	0.80	0.85	0.85	0.95	0.90
E	0.80	0.80	0.80	0.90	0.80	1.00	0.90
SE	0.80	0.95	0.80	0.90	0.80	0.95	0.90
S	0.85	0.90	0.80	0.95	0.85	0.85	0.90
SW	0.95	0.95	0.85	0.95	0.90	0.95	0.90
W	1.00	1.00	0.90	0.95	1.00	1.00	1.00
NW	0.95	0.95	1.00	0.90	0.95	0.95	1.00

2.4.4. Terrain/height multiplier (M_z,cat)

The terrain/height multiplier (Table 3) is used to acount for variation in wind speed with variation in height and terrain roughness. According to AS/NZS 1170.2 standard, terrain can be classified into four categories.

• Category 1: open terrain and water surfaces with few or no obstructions. Roughness length is about 0.002 m.
• Category 2: open terrain, grassland and water surfaces with few well scattered obstructions with heights from 1.5 m to 10 m. Roughness length is about 0.02 m.
• Category 3: terrain with numerous closely spaced obstructions 3 to 5 m high such as suburban housing. Roughness length is about 0.2 m.
• Category 4: terrain with numerous large, high (10 m to 30 m) and closely spaced obstructions such as large cities and well-developed industrial complexes. Roughness length is about 2 m.

Table 3. Terrain/height multiplier (AS/NZS 1170.2 standard).

Height, m	1		2		3		4
	non-cyclonic	cyclonic	non-cyclonic	cyclonic	non-cyclonic	cyclonic	non-cyclonic	cyclonic
≤ 3	0.99	0.90	0.91	0.90	0.83	0.80	0.75	0.80
5	1.05	0.95	0.91	0.95	0.83	0.80	0.75	0.80
10	1.12	1.00	1.00	1.00	0.83	0.89	0.75	0.89
15	1.16	1.07	1.05	1.07	0.89	0.95	0.75	0.95
20	1.19	1.13	1.08	1.13	0.99	1.05	0.75	1.05
30	1.22	1.20	1.12	1.20	1.00	1.15	0.80	1.15

For intermediate values of height and terrain category, AS/NZS 1170.2 recommends to use linear interpolation.

2.4.5. Shielding Multiplier (M_s)

The shielding multiplier (Table 4) is used to account for the shielding effect from upwind buildings that are either taller or the same height as the building being considered [4]. The shielding multiplier is equal to 1.0 for open country.

Table 4. Shielding multiplier (AS/NZS 1170.2 standard).

Terrain class	Shielding multiplier
City buildings	0.90
High density metro	0.88
Suburban	0.85
Other	1.00

The shielding multiplier has to be adjusted if a building is standing on a slope and a prevalent wind direction is consistent with the direction of the slope. When the average upwind ground gradient is grater than 20%, the shielding multiplier is equal to 1.0. If the average upwind ground gradient is less than 5%, the adjustment of the shielding multiplier is not required. The linear interpolation is used for the slope values between 5.5% and 22%.

2.4.6. Topographic multiplier (M_t)

The topographic multiplier is used to account for the effect of topography on the wind speed. In mainland Australia, the topographic multiplier is equal to hill-shape multiplier, which depends on the hill shape and the proximity of the site to the hill crest. The hill-shape multiplier is equal to 1.0 for the slopes below 5% and 1.71 for the slopes grater than 45% (24.2 degrees). The hill-shape multipliers for the slopes between 5% and 45% are shown in Table 5.

Table 5. Hill-shape multiplier at crest (AS/NZS 1170.2 standard).

Hill slope (fractions)	Hill slope (degrees)	Hill-shape multiplier
< 0.05	< 2.9	1.00
0.05	2.9	1.08
0.10	5.7	1.16
0.20	11.3	1.32
0.30	16.7	1.48
≥ 0.45	≥ 24.2	1.71

2.4.7. VIG deflection in response to Wind Load

Knowing the dynamic wind pressure (equation 51), we can estimate the VIG deflection in response to Wind Load using equations 2.18 and 2.20. For the uniformly spread load, q(x, y) = q = const, the coefficients a_ij are defined as $${a_{ij}}={{4\over{L_xL_y}}\int_0^{L_x}\int_0^{L_y}q(x,y)sin{i{\pi}x\over{L_x}}sin{i{\pi}y\over{L_y}}dxdy}={16q\over{{\pi}^2ij}} \tag{2.46}\label{eq2.46} $$ and the equation 2.18 becomes $${W(x,y)}={{16q\over{{\pi}^6D}}\sum_{i=1}^{\infty}\sum_{j=0}^{\infty}{sin{i{\pi}x\over{L_x}}sin{i{\pi}y\over{L_y}}\over{ij({i^2\over{L_x^2}}+{j^2\over{L_y^2}})^2}}} \tag{2.47}\label{eq2.47}$$ Then, we use the same logic as in Debris Load section and calculate the deflection of the plates with h_glass and 2h_glass thicknesses to account for the composite structure of the VIG (equation 2.33).

After calculation of the bending moment coefficients in x- and y-directions (M_x and M_y, respectively) and rotational force (H), we can estimate bending stresses σ_x and σ_y and tangential stress τ_xy. $${M_x}={-{E\over{1-{\mu}^2}}({{{\partial}^2W}\over{{\partial}x^2}}+{\mu}{{{\partial}^2W}\over{{\partial}y^2}}){\int_{-h/2}^{h/2}}z^2dz} \tag{2.48}\label{eq2.48} $$ $${M_y}={-{E\over{1-{\mu}^2}}({{{\partial}^2W}\over{{\partial}y^2}}+{\mu}{{{\partial}^2W}\over{{\partial}x^2}}){\int_{-h/2}^{h/2}}z^2dz} \tag{2.49}\label{eq2.49} $$ $${H}={-{E\over{1-{\mu}^2}}{{\partial}^2W\over{{\partial}x{\partial}y}}{\int_{-h/2}^{h/2}}z^2dz} \tag{2.50}\label{eq2.50} $$ $${{\sigma}_x} ={{12M_xz}\over{h^3}} \tag{2.51}\label{eq2.51} $$ $${{\sigma}_y} ={{12M_yz}\over{h^3}} \tag{2.52}\label{eq2.52} $$ $${{\tau}_{xy}}={{12Hz}\over{h^3}} \tag{2.53}\label{2.53} $$ where h is the plate thickness. The bending moment coefficients are the highest in the center of the plate, where x = L_x/2 and y = L_y/2. For the square plates, M_x = M_y. The maximum bending stresses are observed at z = ± h/2.

2.5. Noise Insulation

UNDER CONSTRUCTION

3. Establishing a Vacuum

In the absence of outgassing, the pressure in the VIG decreases linearly with time in the viscous flow regime, while in the molecular flow regime, the pressure decreases exponentially with time [46]. The type of flow regime is defined by the difference between the mean free path of gas molecules (μ) and the gap size between the two glass panes in the VIG (g):

• at μ << g, the flow is viscous and the collisions between gas molecules are frequent,
• at μ ≈ g, the transition region is observed,
• at μ >> g, the flow is molecular and inter-molecular collisions are rare.

The mean free path depends on gas pressure (P), temperature (T) and diameter of gas molecule (d): $${\mu}={{k_BT}\over{\sqrt{2}{\pi}d^2P}} \tag{3.1}\label{eq3.1} $$ where k_B is the Boltzmann constant. For example, the typical mean free path of air at room temperature and pressure between 220 Torr and 0.8 Torr is 0.1 – 100 μm. In this case, the molecular flow regime is reached at gas pressures below about 0.1 Torr for a gap of 0.1 mm.

The time required to evacuate the VIG internal volume (V) from atmospheric pressure to the transition pressure is approximately equal to the time constant of the exponential pressure decrease in the molecular flow regime. This time constant (τ) is defined as: $${\tau}={V\over{C_{total}}} \tag{3.2}\label{eq3.2} $$ This equation is valid when the pressure within the enclosed region is uniform at any time. C_total is the series combination of the conductance associated with the radially inwards gas flow towards the pump out port (C_eff) and the conductance of the pump out tube (C_tube): $${1\over{C_{total}}} = {{1\over{C_{eff}}}+{1\over{C_{tube}}}} \tag{3.3}\label{eq3.3} $$ $${C_{tube}}={194\sqrt{T\over M}}{{{\pi}d_{tube}^3}\over{16l_{tube}}} \tag{3.4}\label{eq3.4} $$ where M is the mass of the gas molecules in atomic mass units, d_tube is pump out tube diameter and l_tube is tube length.

For a square sample with side length L and a pump out tube near one corner at distance l from adjacent edges, the gas flow pattern can be approximately divided into two parts:

• near the pump out tube, the flow is roughly radially inwards towards the tube over full 2π radian angular range;
• far from the pump out tube, the flow is radially inwards towards the tube over a π/2 radians angular range.

The approximate conductance of the whole sample can be calculated as the series combination of the conductances of these two regions. $${1\over{C_{eff}}} = {{1\over{C_1}}+{1\over{C_2}}} \tag{3.5}\label{eq3.5} $$ where C₁ is the conductance in the region near the pump out tube and C₂ is the conductance in the rest of the sample. $${C_1}=194{\sqrt{T\over M}}{{{\pi}g^2}\over{ln({l/{l_{tube}}})}} \tag{3.6}\label{eq3.6} $$ $${C_2}=194{\sqrt{T\over M}}{{{\pi}g^2}\over{4ln({L/{2l}})}} \tag{3.7}\label{eq3.7} $$ The time (t) required to reach specific pressure (P₀) inside the VIG can be defined as $$t={\tau}(ln(P_{transition}/{P_0})+1) \tag{3.8}\label{eq3.8} $$ where P_transition is the gas pressure of the transition region.

4. Optical Performance

5. Vacuum Stability